数学建模四大模型总结（二）

四大类题型

预测类

指的是通过分析已有的数据或者现象，找出其内在发展规律，然后对未来情形做出预测的过程。
根据已知条件和求解目的，往往将预测类问题分为：
小样本内部预测，大样本内部预测，小样本未来预测，大样本随机因素或周期特征的未来预测，大样本的未来预测。
（分析：预测问题主要是以某个小问的形式出现，很少有整个赛题所有小问全是预测要求的，但是也建议认真对待）

评价类

每个行业都有它的评价标准和准则，那么这些标准应该有其自身的形成机制，数学模型就是形成这一机制的方法.
如何根据成分指标评价一瓶葡萄酒？如何根据员工表现评价年终奖评定？如何评价一名NBA球员在球场上的效率？这些问题都需要设计评价算法来对这些对象进行评价。
保证最后的评价结果最能反映对象的需求同时与标准结果的比较差别最小
（分析：解决评价类赛题的关键是指标体系的构建，构建完评价体系后在选择合适的评价方法即可，体系建立应秉承全面，准确，独立的三要素）

机理分析类赛题

所机理分析是根据对现实对象特性的认识，分析其因果关系，找出反映内部机理的规律。在求解机理分析类问题时首先需要探寻与问题相关的物理，化学，经济等相关的知识，然后通过对已知数据或现象的分析对事物的内在规律做出必要的假设，最后通过构建合适的方程或关系式对其内在规律进行数值表达。
（分析：机理分析立足于建立事物内部的规律，相对于其他类型的赛题均有章可循，机理分析类赛题往往需要结合众多关联知识才可以进行求解，如空气动力学，流体力学，热力学等）

优化类

指在现有现有条件固定的情况下，如何使目标效果达到最佳。如在一座城市公交车公司拥有的公交车数量是固定的，问如何安排线路能够使盈利达到最高。优化类问题往往需要分析三个关键因素：目标函数，决策变量和约束条件，三者往往缺一不可。
（分析：解决优化类赛题必须知道优化的目的，约束的条件和所求解的关键变量，需要有较强的编程能力和赛题分析挖掘能力）

数学建模算法

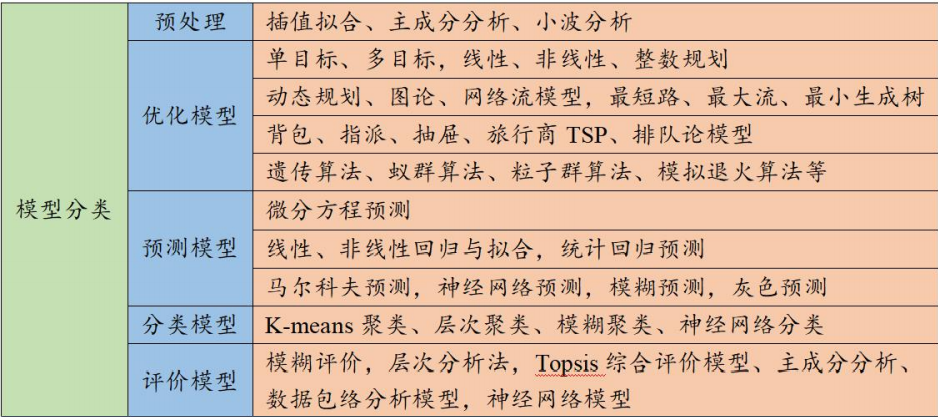
优化类问题

数学规划模型

适用情况：要求一些变量有限制后，某一个变量或结果最大或最小，一般是最值问题，包括：线性规划、整数线性规划、非线性规划、多目标规划、动态规划。

1. 线性规划模型：目标函数和约束条件都是线性函数的数学规划模型；
2. 整数规划模型：决策变量要求取整数值的线性规划模型；
3. 非线性规划模型：目标函数或者约束条件中有非线性函数的数学规划模型；
4. 多目标规划模型：具有多个目标函数的数学规划模型

微分方程组模型

经常适用于人口预测，求最值极值点则为优化的目标

图论算法

最短路径问题、网络最大流问题、最小费用最大流问题、最小生成树问题(MST)、旅行商问题(TSP)、图的着色问题

评价类问题

层次分析法

是最基本的评价问题分析方法，能够求出某个因素的权重。以看出指标的影响力。有权重，用层次分析，分析指标
主观性比较强，要自己定指标，所以一般是辅助问题。

TOPSIS法

TOPSIS法根据有限个评价对象与理想化目标的接近程度进行排序的方法，是在现有的对象中进行相对优劣的评价。
可以加入熵权法分析权重

主成分分析

在实际问题中，研究多指标(变量)问题是经常遇到的，然而在多数情况下，不同指标之间是有一定相关性。由于指标较多并且指标之间有一定的相关性，势必增加了分析问题的复杂性。
数据降维，方便计算，指标太多，减少点
主成分分析就是设法将原来众多具有一定相关性的指标(比如p个指标)，重新组合成一组新的相互无关的综合指标来代替原来指标。通常数学上的处理就是将原来p个指标作线性组合，作为新的综合指标

模糊评价

运用模糊综合评价法可以有效的 将一些定性指标进行定量化分析
比如，A大坝建设的过程中融资可能出现多个风险因素，而每个风险因素对A大坝的影响程度无法进行精准的量化评估，具有一定的模糊特征。基于此，采用模糊综合评价法对A大坝融资过程中可能发生的不确定性进行量化评估

预测类问题

一般的抽象系统，如社会系统、经济系统、农业系统、生态系统等都包含有众多的因素来共同决定了该系统的发展态势，所以系统分析就是要找出哪些是主要因素，那些事次要因素，那些因素对系统发展的影响最大，那些因素对系统发展的影响最小，那些因素对系统发展起推动作用不要强化发展，哪些因素对系统发展起阻碍作用要加以抑制

回归分析

当样本个数n较大时，一般使用标准化回归,做数据拟合，算参数

微分方程预测

一般适用于短中期预测。
例如：
传染病的预测模型、经济增长（或人口）的预测模型、Lanchester战争预测模型、药物在体内的分布与排除预测模型、烟雾的扩散与消失模型
构建方程，拟合参数

主成分分析

灰色关联分析

作用：给出各个指标和结果，算权重，得到哪个影响力大。
可以是预测也可以是评价某个指标
当样本数n较少时，才使用灰色关联分析。
最后得出的灰色关联度在经过归一化后即为各个指标的权重。
到这一步得出的权重，谁的值大，那么哪个指标对系统的影响就大

元胞自动机

一般以分子的方式模拟一些情况的变化。有益于当题目中分析不到指标，或者指标太过于抽象和学术时，以分子的形式创建指标。

神经网络模型 贝叶斯预测模型

小样本情况用贝叶斯预测模型
大样本用神经网络模型比较准确

分类和聚类

一般是子问题需要做的一个步骤，常见的是，将大量的数据结果产生分类。

数学建模 — Jan 31, 2023